在本篇文章中，我们对LCS、LIS问题和两种问题互相转化的条件进行了讨论。

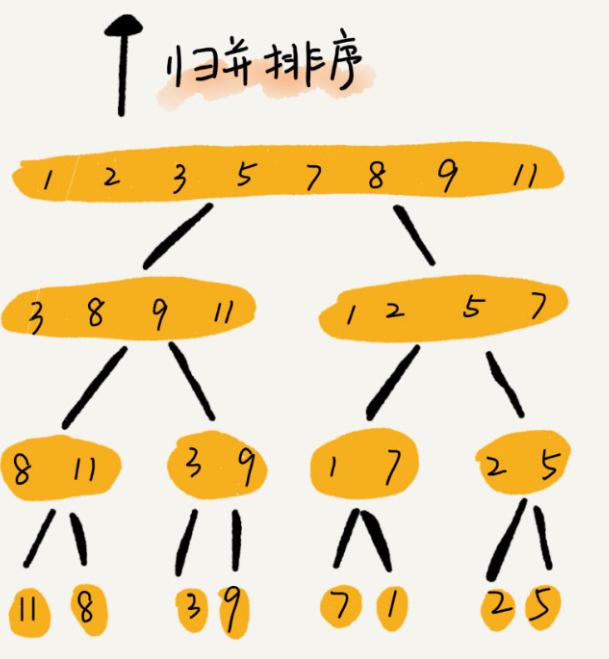
最长公共子序列：动态规划

时间复杂度：O(n * m)

题目描述

/*
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列返回0。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的公共子序列是这两个字符串所共同拥有的子序列。
*/

本题是一道经典的dp问题。

在本题中，我们根据状态转移方程定义不同有两种写法：

// 第一种
// dp[i][j] 定义：dp[i][j]为 text1中0~i-1 和 text2中0~j-1中公共串最长长度。
// 此时，初始化数组则为
dp[0][i] = 0;
dp[i][0] = 0;
// 状态转移方程：对于dp[i][j]：
// 当字符串1与字符串2的i - 1, j - 1字符相等时
dp[i][j] = dp[i – 1][j – 1] + 1;
// 当字符串i – 1, j – 1字符不等时，则
dp[i][j] = max(dp[i – 1][j], dp[i][j – 1]);


// 第二种
// dp[i][j] 定义： dp[i][j]为 text1中0~i 和 text2中0~j中公共串最长长度
// 此时，初始化数组则有变化：
// 如果text1[i] == text2[0] 说明从此开始到之后的所有字符串均含有公共字符		text2[0]，所以从此以后都应赋值为1。而如果不等，则继续向后比较。

// 状态转移方程
// 对于dp[i][j]：
if (text1[i] == text2[j]) dp[i][j] = dp[i – 1][j – 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

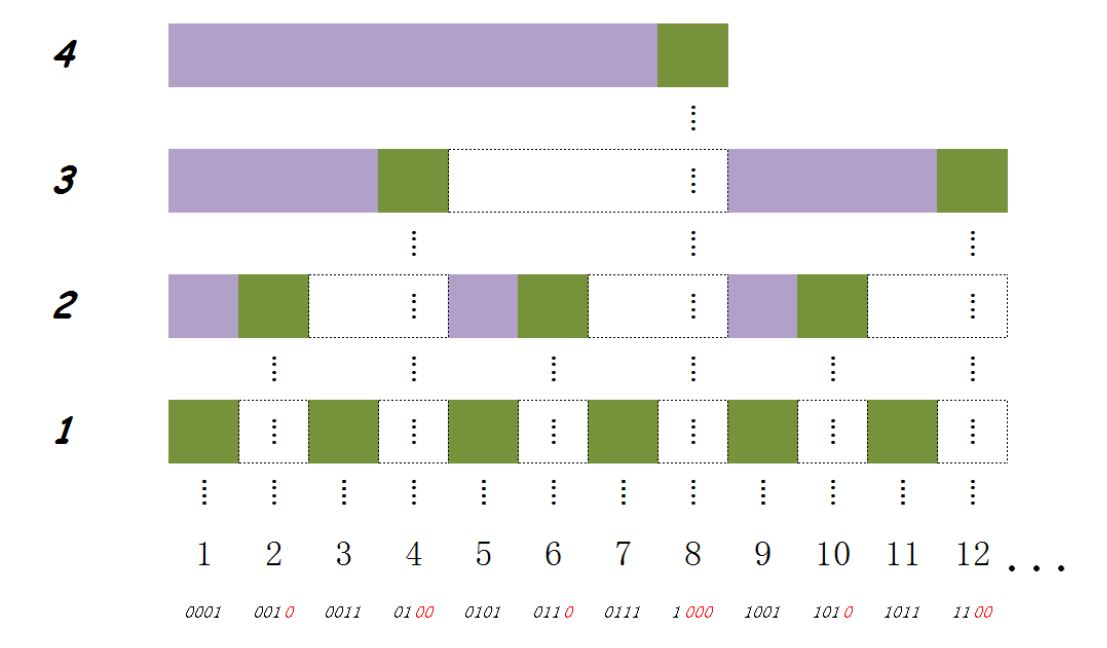
最长上升子序列：贪心+二分法

时间复杂度：O(nlogn)

举例：Leetcode 334. 递增的三元子序列

题目描述

/*
给你一个整数数组 nums ，判断这个数组中是否存在长度为 3 的递增子序列。

如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ，使得 nums[i] < nums[j] < nums[k] ，返回true ；否则，返回 false 。
*/

本题可以使用时间复杂度O(n)的纯贪心策略才做，通过维护first, second和 last 三个变量来寻找。
为了说明LIS问题，本题我们求出最大的递增子序列并判断与3的关系。
- 我们在遍历每一个nums[i]时，维护一个具有单调性的数组f[]
- 其中，f[len] = x代表长度为len的最长上升子序列最小的结尾元素为x
- 因此可以每次通过二分法找到小于nums[i]的最大下标，来作为nums[i]的前一个数。

class Solution {
    public boolean increasingTriplet(int[] nums) {
        int[] f = new int[nums.length + 1];
        int ans = 1;
        Arrays.fill(f, Integer.MAX_VALUE);
        for (int i = 0; i < nums.length; i++) {
            int t = nums[i];
            int l = 1, r = i + 1;
            while (l < r) {
                int mid = (l + r) / 2;
                if (f[mid] >= t) r = mid;
                else l = mid + 1;
            }
            f[r] = t;
            ans = Math.max(ans, r);
        }
        return ans >= 3;
    }
}

LCS 问题与 LIS 问题的相互关系

举例：Leetcode1713. 得到子序列的最少操作次数

题目描述

/*
给你一个数组 target ，包含若干互不相同的整数，以及另一个整数数组arrarr可能包含重复元素。

每一次操作中，你可以在arr的任意位置插入任一整数。比方说，如果 arr = [1,4,1,2] ，那么你可以在中间添加 3 得到 [1,4,3,1,2] 。你可以在数组最开始或最后面添加整数。

请你返回最少操作次数，使得 target 成为 arr 的一个子序列。

一个数组的子序列 指的是删除原数组的某些元素（可能一个元素都不删除），同时不改变其余元素的相对顺序得到的数组。比方说，[2,7,4] 是 [4,2,3,7,2,1,4] 的子序列（加粗元素），但 [2,4,2] 不是子序列。
*/

解题思路
- 我们可以令target的长度为n，arr的长度为m，target和arr的最长公共子序列长度为max，我们可以发现最终答案为n – max。
- 此题便变成了LCS问题。
- 但是朴素LCS问题求解会超时。
- 一个很显眼的切入点是：target数组元素各不相同，当 LCS 问题增加某些条件限制之后，会存在一些很有趣的性质。
- 当其中一个数组元素各不相同时，LCS问题可以转换为LIS进行求解。同时LIS存在使用贪心+二分解法，复杂度为O(nlogn)。
- 本题可以通过
  - 抽象成LCS问题
  - 利用target数组元素各不相同，转换为LIS问题
  - 使用LIS贪心+二分解法，时间复杂度可以达到O(nlogn)
- 有些隐晦，我们举个例子：
  - ~~我能和你一起吃饭吗赵宝~~

/*
tar = [6, 4, 8, 1, 3, 2],  arr = [4, 7, 6, 2, 3, 8, 6, 1]
因为我们只涉及给arr添加元素，最终答案也与arr无关，所以我们将arr中没在tar出现的元素去掉
tar = [6, 4, 8, 1, 3, 2], arr' = [4, 6, 2, 3, 8, 6, 1]
这时候注意到tar中元素无重复, 这个性质就像是索引一样, 我们当然就可以把他们当成索引, 得到一个新性质: 有序
idx = [0, 1, 2, 3, 4, 5]
tar = [6, 4, 8, 1, 3, 2]
这样, 
tar' = [0, 1, 2, 3, 4, 5]
arr' = [1, 0, 5, 4, 2, 0, 3]
其中tar'是递增的顺序集合, 而arr'是一种乱序集合
这时候我们只需要找到arr'中最长的符合严格单调递增性质的子序列lis长度即可

代码：

class Solution {
    public int minOperations(int[] target, int[] arr) {
        int n = target.length, m = arr.length;
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            map.put(target[i], i);
        }
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < m; i++) {
            int x = arr[i];
            if (map.containsKey(x)) list.add(map.get(x));
        }
        int len = list.size();
        int[] f = new int[len], g = new int[len + 1];
        Arrays.fill(g, Integer.MAX_VALUE);
        int max = 0;
        for (int i = 0; i < len; i++) {
            int l = 0, r = len;
            while (l < r) {
                int mid = (l + r + 1) / 2;
                if (g[mid] < list.get(i)) l = mid;
                else r = mid - 1;
            }
            int clen = r + 1;
            f[i] = clen;
            g[clen] = Math.min(g[clen], list.get(i));
            max = Math.max(max, clen);
        }
        return n - max;
        
    }
}