概率论的基础知识

本篇文章，从条件概率开始复习，通过条件概率的可列可加性推出全概率公式与贝叶斯公式，最后得到先验概率与后验概率的概念。

条件概率

定义

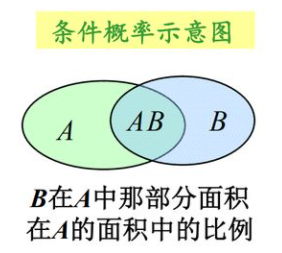
在一个事件已经发生的情况下，另一事件发生的概率。

$P(B|A)\ne P(B)$

$P(B|A)$ 叫做A发生的条件下B发生的概率，称为条件概率。

根据古典概型的概率计算模型，已知A发生的条件下，B发生的概率为：

$P(B|A) = \displaystyle\frac{P(AB)}{P(A)}$

性质

非负性
规范性
可列可加性：
- 设 $B1, B2,\dots$ 两两不相容，
- $P(\bigcup_{i=1}^{\infty}B_{i})|A) = \frac{P[A(\bigcup_{i=1}^{\infty}B_{i}))]}{P(A)} = \frac{P[(\bigcup_{i=1}^{\infty}AB_{i}))]}{P(A)}=\frac{\sum_{i=1}^{\infty}P(AB_{i})}{P(A)} = \sum_{i = 1}^{\infty}\frac{P(AB_{i})}{P(A)}=\sum_{i = 1}^{\infty}P(B_{i}|A)$

由于条件概率满足概率三条件，有关概率的重要结果与运算律均对条件概率成立。

乘法公式

$P(AB)=P(A)P(B|A)$

$P(A_{1}A_{2}A_{3})=P(A_{1})P(A_{2}|A_{1})P(A_{3}|A_{1}A_{2})$

更一般的：

$P(A_{1}A_{2}\dots A_{n}) = P(A_{1})P(A_{2}|A_{1})P(A_{3}|A_{1}A_{2})\dots P(A_{n}|A_{1}A_{2}\dots A_{n-1})$

$(P(A_{1}A_{2}\dots A_{n-1})>0)$

意义：当我们容易求的事件A的概率时，乘法公式就能求得A、B同时发生的概率。

全概率公式

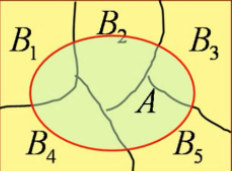
设试验E的样本空间为S，且 $B_{1},B{2},\dots,B_{n}$ 为S的一个划分（完备事件组）

全概率公式：

$P(A) = P(B_{1})P(A|B_{1})+P(B_{2})P(A|B_{2})+\dots+P(B_{n})P(A|B_{n})$

意义

将复杂事件A划分为较简单的事件 $AB_{1}\dots AB_{n}$ ，再结合加法公式和乘法公式计算出A的概率。

可以形象的把全概率公式看作是由原因溯结果，每个原因对结果的发生都有一定的作用。

贝叶斯公式

$P(B|A) = \displaystyle\frac{P(B)P(A|B)}{P(A)}$

$P(B_{i}|A) = \displaystyle\frac{P(B_{i})P(A|B_{i})}{\sum_{j=1}^n P(B_{j})P(A|B_{j})}$

注：通过条件概率与全概率公式推导，上面为 $P(AB_{i})$ ，下面为 $P(A)$

意义

在事件A已经发生的条件下，贝叶斯公式可用来寻找导致A发生的各种原因 $B_{i}$ 的概率。

先验概率与后验概率

先验概率：指根据以往经验分析，实验或采样前便可以得到的概率。

后验概率：指某件概率已经发生，想要计算这件事发生的原因是由于某个因素引起的概率。

举例

假设我们现在有两个盒子，分别为红色和蓝色。在红色盒子中放着2个苹果和6个橙子，在蓝色盒子中放着1个橙子和3个苹果，如下图所示：

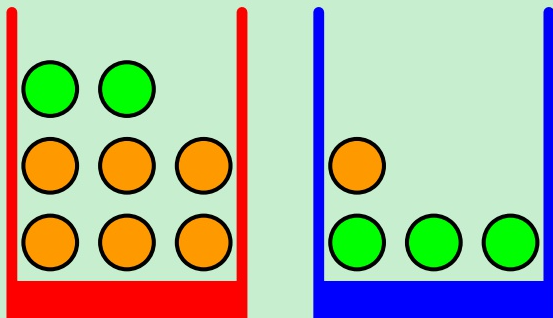
图中绿色表示苹果，橙色代表橙子。假设我们每次实验的时候会随机从某个盒子里挑出一个水果，随机变量B（box）表示挑出的是哪个盒子，并且P(B=blue) = 0.6（蓝色盒子被选中的概率），P(B=red) = 0.4（红色盒子被选中的概率）。随机变量F（fruit）表示挑中的是哪种水果，F的取值为"a (apple)“和"o (orange)”。

如果我们已知某次实验挑出来的是orange，这个orange从红色盒子挑出来的概率？

$P(B=red|F=o) = \displaystyle\frac{P(F=o|B=red)P(B=red)}{P(F=o)} = \frac{2}{3}$