第五章 线性方程组

线性方程组解的存在性

齐次线性方程组有非零解的充要条件

  1. m×nm×n型齐次线性方程组Ax=0Ax=0有非零解（只有零解）⇔r(A)<n\Leftrightarrow r(A)<n (r(A)=n)(r(A)=n)

    • 注：r(A)<nr(A)<n意味着将A化为行阶梯阵时非零行的个数小于n，即对方程Ax=0Ax=0化简以后所留下方程的个数小于n。一个方程只能确定一个未知数，这时有自由变化的未知数，所以有非零解。

    • 直观描述：由于Ax=0Ax=0，所以如果和某个x有关，则使得Ax=0的取指只能是0，如果是别的数则不能都满足=0的条件（前后违背），但是如果和某个x无关，则可以在这个x上随便取值，反正无关，取多少Ax都等于0.

非齐次线性方程组解的存在性

对于非齐次线性方程组，可能有解，也可能无解；有解时可能是唯一解，也可能是无穷多个解。

  1. 设Ax=bAx=b是m×nm×n型非齐次线性方程组，则
    1. Ax=bAx=b有无穷多解⇔r((A,b))=r(A)<n\Leftrightarrow r((A,b))=r(A)<n
    2. Ax=bAx=b有唯一解⇔r((A,b))=r(A)=n\Leftrightarrow r((A,b))=r(A)=n
    3. Ax=bAx=b无解⇔r((A,b))>r(A)\Leftrightarrow r((A,b))>r(A)
      • 注：⇔r((A,b))>r(A)\Leftrightarrow r((A,b))>r(A)表示化为行阶梯式后可能会出现0x1+0x2+⋯+0xn=b0x_1+0x_2+\dots+0x_n=b，显然无解。

线性方程组解的性质、结构与解法

线性方程组解的性质

  1. 若v1,v2,…,vsv_1,v_2,\dots,v_s为齐次线性方程组Ax=0Ax=0的解，则k1v1+k2v2+⋯+ksvsk_1v_1+k_2v_2+\dots+k_sv_s也为Ax=0Ax=0的解，其中k1,k2,…,ksk_1,k_2,\dots,k_s为任意常数。
  2. 若uu为非齐次线性方程组Ax=bAx=b的解，vv为Ax=0Ax=0的解，则u+vu+v为Ax=bAx=b的解。
  3. 非齐次线性方程组Ax=bAx=b的两个解u1u1和u2u2的差为u1−u2u1-u2为Ax=0Ax=0的解。
  4. 若u1,u2,…,usu_1,u_2,\dots,u_s为非齐次线性方程组Ax=bAx=b的解，则
    1. k1u1+k2u2+⋯+ksusk_1u_1+k_2u_2+\dots+k_su_s为Ax=bAx=b的解⇔∑i=1ski=1\Leftrightarrow\sum_{i=1}^{s}k_i=1
    2. k1u1+k2u2+⋯+ksusk_1u_1+k_2u_2+\dots+k_su_s为Ax=0Ax=0的解⇔∑i=1ski=0\Leftrightarrow\sum_{i=1}^{s}k_i=0

齐次线性方程组解的结构

  1. 齐次线性方程组Ax=0Ax=0的解集S（即全部解向量的集合）的极大无关组叫做该齐次线性方程组的基础解系。
    • 若已知Ax=0Ax=0的基础解系为v1,v2,…,vsv_1,v_2,\dots,v_s，则由定理可知，Ax=0Ax=0的通解为x=k1v1+k2v2+⋯+ksvsx=k_1v_1+k_2v_2+\dots+k_sv_s，其中k1,k2,…,ksk_1,k_2,\dots,k_s为任意常数。
  2. （确定齐次方程组的基础解系）齐次方程组Ax=0Ax=0的解集S的秩为r(S)=n−r(A)r(S)=n-r(A)，即Ax=0Ax=0的基础解系所含向量的个数为n−r(A)n-r(A)，其中n为未知数的个数，即A的列数。
    • 即解系的秩为和Ax=0无关的那些x的数目。
  3. r(AAT)=r(A)=r(AT)r(AA^T)=r(A)=r(A^T)

非齐次方程解的结构

  1. 设uu为非齐次线性方程组Ax=bAx=b的一个已知解（称为特解），v1,v2,…,vn−rv_1,v_2,\dots,v_{n-r}为Ax=0Ax=0的基础解系，则Ax=bAx=b的通解为x=k1v1+k2v2+⋯+kn−rvn−r+ux=k_1v_1+k_2v_2+\dots+k_{n-r}v_{n-r}+u，其中，k1,k2,…,knk_1,k_2,\dots,k_n为任意常数。
    • 即非齐次线性方程组的通解=对应的齐次线性方程组的通解+该非齐次线性方程组的一个特解

利用矩阵初等行变换解线性方程组

第六章 向量空间及向量的正交性

向量空间

定义

  1. 设V是n元向量的集合，如果V非空，并且对于向量的线性运算封闭，则称V是一个向量空间。
    • 齐次线性方程组Ax=0Ax=0的所有解向量构成的集合S是一个向量空间
    • 若V是向量空间，则V一定含有零向量
    • 由于非齐次线性方程组Ax=bAx=b的解集不含有零向量，所以Ax=bAx=b的解集不是向量空间。
  2. 设V1V_1和V2V_2是两个向量空间，若V1⊆V2V_1\subseteq V2，则称V1V_1是V2V_2的子空间；若V1⊆V2&&V2⊆V1V_1\subseteq V2 \&\& V_2\subseteq V1，则称这两个向量空间相等，记作V1=V2V_1=V_2

向量空间的基与维数

  1. 向量空间V的一个极大无关组叫做V的一个基，V的秩叫做V的维数，记作dim(V)dim(V)，若dim(V)=rdim(V)=r，则称V为r维向量空间。
    • 若已知r维向量空间V的基为v1,v2,…,vrv_1,v_2,\dots,v_r，则称向量空间可表示为V={v=x1v1+x2v2+⋯+xrvr∣x1,…,xr∈R}V=\{ v=x_1v_1+x_2v_2+\dots+x_rv_r|x1_,\dots,x_r\in R\}
  2. 设V是n维向量空间，m<nm<n，则V中任一线性无关向量组v1,v2,…,vmv_1,v_2,\dots,v_m都可扩充成V的一个基。

向量在基下的坐标

  1. 设a1,a2,…,ana_1,a_2,\dots,a_n是n维向量空间V的一个基，对任一向量b∈Vb\in V，把满足b=x1a1+x2a2+⋯+xnanb=x_1a_1+x_2a_2+\dots+x_na_n的有序数x1,x2,…,xnx_1,x_2,\dots,x_n叫做向量b在这个基下的坐标。x=(x1,x2,…,xn)Tx=(x_1,x_2,\dots,x_n)^T叫做向量b在这个基下的坐标向量。

过渡矩阵与坐标变换

  1. 设n维向量空间V中的向量v在旧基a1,a2,…,ana_1,a_2,\dots,a_n和新基b1,b2,…,bnb_1,b_2,\dots,b_n下的坐标向量分别为x和y，从旧基到新基的过渡矩阵为P，则有坐标变换公式：x=Pyx=Py，即y=P−1xy=P^{-1}x

    • 证明：已知得：

      {B=APv=Ax(A=(a1,a2,…,an),x=(x1⋮xn))v=By=APy\left\{\begin{aligned}B&=AP\\ v&=Ax(A=(a_1,a_2,\dots,a_n),x=\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix})\\ v&=By=APy\end{aligned}\\\right.

      于是(3)-(2)得

      A(Py−x)=OA(Py-x)=O

      并由a1,a2,…,ana_1,a_2,\dots,a_n线性无关可得，r(A)=nr(A)=n

      于是r(Py−x)=0r(Py-x)=0，即x=Pyx=Py，得证。

向量的正交性

向量的内积

  1. 设a=(a1,a2,…,an)T,b=(b1,b2,…,bn)Ta=(a_1,a_2,\dots,a_n)^T,b=(b_1,b_2,\dots,b_n)^T是两个实向量，aa与bb的内积记作(a,b)(a,b)，规定(a,b)=a1b1+a2b2+⋯+anbn(a,b)=a_1b_1+a_2b_2+\dots+a_nb_n，也可用矩阵运算表示内积：(a,b)=aTb=bTa(a,b)=a^Tb=b^Ta
  2. 其中，a,b,c∈Rn,a,b,c\in R^n,k为任意实数，则内积有如下性质：
    • (a,b)=(b,a)(a,b)=(b,a)
    • (ka,b)=k(a,b)(ka,b)=k(a,b)
    • (a+b,c)=(a,c)+(b,c)(a+b,c)=(a,c)+(b,c)
    • (a,a)≥0(a,a)\ge0且a=0⇔(a,a)=0a=0\Leftrightarrow(a,a)=0
  3. 定义了内积的实向量空间称为欧几里得空间，简称欧氏空间。
  4. 实向量a=(a1,a2,…,an)Ta=(a_1,a_2,\dots,a_n)^T的长度定义为：∣∣a∣∣=(a,a)=a12+a22+⋯+an2||a||=\sqrt{(a,a)}=\sqrt{a_1^2+a_2^2+\dots+a_n^2}，当∣∣a∣∣=1||a||=1时，aa叫做单位向量；对于非零向量aa，称a∣∣a∣∣\dfrac{a}{||a||}为a的单位化向量。
    • 注：aTa=∣∣a∣∣2a^Ta=||a||^2
  5. 向量长度的性质：
    • 非负性 ∣∣a∣∣≥0||a||\ge0且∣∣a∣∣=0⇔a=0||a||=0\Leftrightarrow a=0
    • 齐次性 ∣∣ka∣∣=∣k∣∣∣a∣∣||ka||=|k|\enspace||a||
    • 三角不等式 ∣∣a+b∣∣≤∣∣a∣∣+∣∣b∣∣||a+b||\le||a||+||b||
    • 施瓦茨不等式 ∣∣(a,b)∣∣≤∣∣a∣∣∣∣b∣∣||(a,b)||\le||a||\enspace||b||
  6. 当a≠0,b≠0a\ne0,b\ne0时，把θ=arccos((a,b)∣∣a∣∣∣∣b∣∣)\theta=arccos(\dfrac{(a,b)}{||a||\enspace||b||})叫做向量a与b的夹角。当(a,b)=0(a,b)=0，即aTb=0a^Tb=0时，称向量a与b正交。

正交基与施密特正交化方法

  1. 由两两正交的非零向量组成的向量组称为正交向量组；由单位向量组成的正交向量组称为标准正交向量组；当向量空间V的一个基为正交向量组时，则称这个基为V的正交基；当V的基为标准正交向量组时，则称这个基为标准正交基。

  2. 正交向量组一定线性无关。

  3. 施密特正交化：设a1,a2,…,ama_1,a_2,\dots,a_m是一个线性无关的向量组，若令

    ​ {b1=a1bj=aj−∑i=1j−1biTaj∣∣bi∣∣2bi\left\{\begin{aligned}b_1&=a_1\\b_j&=a_j-\sum_{i=1}^{j-1}\dfrac{b_i^Ta_j}{||b_i||^2}b_i\end{aligned}\\\right.，则b1,b2,…,bmb_1,b_2,\dots,b_m是与a1,a2,…,ama_1,a_2,\dots,a_m等价的正交向量组。

    将b1,b2,…,bmb_1,b_2,\dots,b_m单位化后可得到一个与a1,a2,…,ama_1,a_2,\dots,a_m等价的标准正交向量组。

正交阵

  1. 若实方阵A满足ATA=EA^TA=E，则称A为正交阵。

    • ATA=E⇔A−1=AT⇔AAT=EA^TA=E\Leftrightarrow A^{-1}=A^T\Leftrightarrow AA^T=E

  2. 正交阵性质：设A、B为同阶正交阵，则

    1. A可逆，且A−1=ATA^{-1}=A^T
    2. ATA^T和A−1A^{-1}都为正交阵
    3. ABAB为正交阵
    4. ∣A∣=±1|A|=±1

  3. 实方阵A为正交阵⇔\LeftrightarrowA的列向量组为标准正交向量组。

    • 证明：ATA=(a1Ta2T⋮anT)(a1,a2,…,an)=(a1Ta1a1Ta2…a1Tana2Ta1a2Ta2…a2Tan⋮⋮⋮anTa1anTa2…anTan)A^TA=\begin{pmatrix}a^T_1\\a_2^T\\\vdots\\a_n^T\end{pmatrix}(a_1,a_2,\dots,a_n)=\begin{pmatrix}a^T_1a_1 & a^T_1a_2 & \dots&a^T_1a_n\\a^T_2a_1 & a^T_2a_2 & \dots&a^T_2a_n\\\vdots &\vdots&&\vdots\\a^T_na_1 & a^T_na_2 & \dots&a^T_na_n\end{pmatrix}，故

      ATA=EA^TA=E的充要条件是aiTai=1,aiTaj=0(i≠j,i,j=1,2,…,n)a_i^Ta_i=1,a_i^Ta_j=0\enspace(i\ne j,\enspace i,j=1,2,\dots,n)

第七章 方阵的特征值与相似对角化

方阵的特征值及其特征向量

特征值与特征向量的概念及计算

  1. 设A为n阶方阵，λ是变量，把∣λE−A∣=0|\lambda E-A|=0的根叫做A的特征值（单根称为单特征值，重根称为重特征值）。

    设λj\lambda_j是A的特征值，则齐次线性方程组(λjE−A)x=0(\lambda_jE-A)x=0的非零解向量叫做A的对应于（或属于）λj\lambda_j的特征向量。

    ∣λE−A∣=0|\lambda E-A|=0称为A的特征方程。

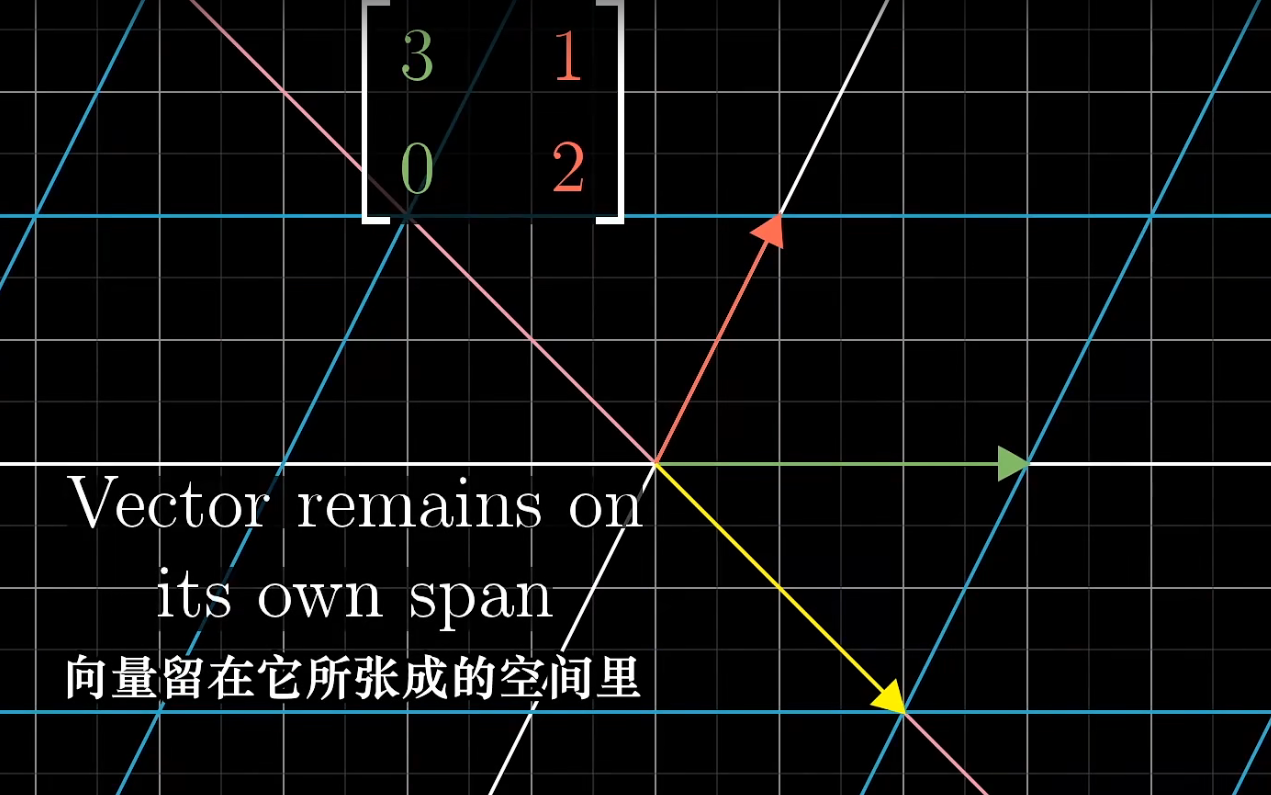
  2. 特征向量的几何意义：变换后仍留在其张成空间内，且变换倍数为其特征值。

    1

    2

特征值与特征向量的性质

  1. n阶方阵A在复数域内有且只有n个特征值（k重特征值看作k个）
  2. ∣λE−A∣|\lambda E-A|称为A的特征多项式，tr(A)tr(A)称作A的迹，其中，设n阶方阵A的特征值为λ1,λ2,…,λn\lambda_1,\lambda_2,\dots,\lambda_n，则
    1. λ1+λ2+⋯+λn=tr(A)\lambda_1+\lambda_2+\dots+\lambda_n=tr(A)
    2. λ1λ2…λn=∣A∣\lambda_1\lambda_2\dots\lambda_n=|A|
  3. 方阵A可逆⇔\LeftrightarrowA的特征值都不为零。
  4. 设A是n阶方阵，则λ是A的特征值且p是λ对应的特征向量⇔\Leftrightarrow数λ和n元非零向量满足Ap=λpAp=\lambda p（这也是很多教材上的特征值与特征向量的定义）
  5. 若λ是方阵A的特征值，p是对应的特征向量，k是正整数，则λk\lambda^k是AkA^k的特征值，pp仍是其对应的特征向量。
  6. 若λ是A的特征值，p是对应的特征向量，则f(λ)=lmλm+lm−1λm−1+⋯+l1λ+l0f(\lambda)=l_m\lambda^m+l_{m-1}\lambda^{m-1}+\dots+l_1\lambda+l_0是f(A)=lmAm+lm−1Am−1+⋯+l1A+l0Ef(A)=l_mA^m+l_{m-1}A^{m-1}+\dots+l_1A+l_0E的特征向值，p仍是其特征向量。
  7. 设λ是可逆阵A的特征值，p是对应的特征向量，则λ−1\lambda^{-1}和∣A∣λ−1|A|\lambda^{-1}分别是A−1A^{-1}和A∗A^*的特征值，p仍是对应的特征向量。
  8. 方阵AA与ATA^T的特征值相同。
  9. 设λ1,λ2,…,λm\lambda_1,\lambda_2,\dots,\lambda_m是方阵A的互异特征值，pi1,pi2,…,pirip_{i1},p_{i2},\dots,p_{ir_i}是λi(i=1,2,…,m)\lambda_i(i=1,2,\dots,m)对应的线性无关的特征向量，则p11,p12,…,p1r1,…,pm1,pm2,…,pmrmp_{11},p_{12},\dots,p_{1r_1},\dots,p_{m1},p_{m2},\dots,p_{mr_m}线性无关。

相似矩阵

相似矩阵的概念与性质

  1. 设A,BA,B为n阶方阵，如果存在n阶可逆阵P，使得P−1AP=BP^{-1}AP=B，则称A与B相似；P−1APP^{-1}AP称为对A进行相似变换，P称为相似变换矩阵。

    如果相似变换矩阵P是正交阵，则称A与B正交相似；P−1APP^{-1}AP称为对A进行正交相似变换。

  2. 相似阵满足自反性、对称性、传递性；

    若A与B相似，则AkA^k与BkB^k相似（k为正整数）

    若A与B相似，则A和B有相同的特征多项式，从而A和B有相同的特征值、行列式以及迹。

相似对角化

  1. 如果矩阵能与对角阵相似，则称A可相似对角化。

    当A可相似对角化时，与A相似的对角阵叫做A的相似标准型。

  2. n阶方阵A可相似对角化的充要条件是A有n个线性无关的特征向量。

    • A相似对角化的相似变换矩阵P是以A的n个线性无关的特征向量为列所构成的矩阵，所化为的对角阵Λ\varLambda的对角元恰为A的n个特征值，并且特征值在Λ\varLambda中的排列次序与特征向量在P中的排列次序相对应。

  3. 若n阶方阵A的特征值都是单特征值，则A可相似对角化。

  4. 设μ\mu是n阶方阵A的k重特征值，p1,p2,…,psp_1,p_2,\dots,p_s是μ\mu对应的线性无关的特征向量，则s≤ks\le k

  5. n阶方阵A可相似对角化的充要条件是A的每个特征值所对应的线性无关特征向量的个数都恰好等于其重数。

  6. n阶方阵A可相似对角化的充要条件是每个特征值λi\lambda_i都满足r(λiE−A)=n−kir(\lambda_iE-A)=n-k_i，其中kik_i为λi\lambda_i的重数。

实对角阵的相似对角化

共轭矩阵

  1. 设A=(aij)m×nA=(a_{ij})_{m×n}为复矩阵，把Aˉ=(aijˉ)m×n\bar{A}=(\bar{a_{ij}})_{m×n}叫做A的共轭矩阵。
    • Aˉˉ=A\bar{\bar A}=A

实对称阵的性质

  1. 实对称阵A的特征值都是实数。
  2. 实对称阵A的相异特征值λ和μ分别对应的特征向量p和q一定正交。
  3. 对于任意n阶实对称阵A，都存在正交阵Q，使得Q−1AQ=diag(λ1,λ2,…,λn)Q^{-1}AQ=diag(\lambda_1,\lambda_2,\dots,\lambda_n)，其中λ1,λ2,…,λn\lambda_1,\lambda_2,\dots,\lambda_n是A的特征值。
  4. 实对称阵的每个特征值所对应的线性无关特征向量的个数恰好等于其重数
  5. 两个同阶的实对称阵相似的充要条件是它们具有相同的特征值。

第八章 二次型

二次型的概念及标准型

二次型的概念及矩阵表示

  1. 关于n个变量x1,x2,…,xnx_1,x_2,\dots,x_n的二次齐次函数f(x1,x2,…,xn)=a11x12+a22x22+⋯+annxn2+2a12x1x2+2a13x1x3+⋯+2an−1,nxn−1xnf(x_1,x_2,\dots,x_n)=a_{11}x_1^2+a_{22}x_2^2+\dots+a_{nn}x_n^2+2a_{12}x_1x_2+2a_{13}x_1x_3+\dots+2a_{n-1,n}x_{n-1}x_n称为n元二次型。

  2. g(y1,y2,…,yn)=d1y12+d2y22+⋯+dnyn2g(y_1,y_2,\dots,y_n)=d_{1}y_1^2+d_{2}y_2^2+\dots+d_{n}y_n^2称为标准二次型

  3. h(z1,z2,…,zn)=z12+z22+⋯+zp2−zp+12−⋯−zp+q2h(z_1,z_2,\dots,z_n)=z_1^2+z_2^2+\dots+z_p^2-z_{p+1}^2-\dots-z_{p+q}^2称为规范二次型

  4. 将二次型写为矩阵形式：

    f(x1,x2,…,xn)=a11x12+a22x22+⋯+annxn2+2a12x1x2+2a13x1x3+⋯+2an−1,nxn−1xnf(x_1,x_2,\dots,x_n)=a_{11}x_1^2+a_{22}x_2^2+\dots+a_{nn}x_n^2+2a_{12}x_1x_2+2a_{13}x_1x_3+\dots+2a_{n-1,n}x_{n-1}x_n

    =(x1,x2,…,xn)(a11a12…a1na21a22…a2n⋮⋮⋮an1an2…ann)(x1x2⋮xn)=(x_1,x_2,\dots,x_n)\begin{pmatrix}a_{11} & a_{12} & \dots&a_{1n}\\a_{21} & a_{22} & \dots&a_{2n}\\\vdots &\vdots&&\vdots\\a_{n1} & a_{n2} & \dots&a_{nn}\end{pmatrix}\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}

    f(x)=xTAxA=(aij)n×n,x=(x1,x2,…,xn)Tf(x) = x^TAx\enspace A=(a_{ij})_{n×n},x=(x_1,x_2,\dots,x_n)^T

    其中，A为对称阵，叫做二次型f(x)的矩阵。

    对称阵A的秩叫做二次型f(x)=xTAxf(x) = x^TAx的秩。

线性变换与相合变换

  1. 设AA和xx分别为m×nm×n型矩阵和nn元列变量，把y=Axy=Ax叫做从n元变量x到m元向量y的线性变换。

    当AA为可逆阵时，y=Axy=Ax叫做可逆变换

    当AA为正交阵时，y=Axy=Ax叫做正交变换。

  2. 正交变换是一种特殊的可逆变换，保持向量的内积、长度和夹角不变，因而在几何空间中保持几何图形不变。

  3. 对于n阶方阵A和B，若存在可逆阵P，使得PTAP=BP^TAP=B，则称A和B相合（也称A和B合同）。变换PTAPP^TAP叫作对A进行合同变换。

    • 推导：对于二次型f(x)=xTAxf(x) = x^TAx进行可逆变换x=Pyx=Py，由

      f(x)=(Py)TA(Py)=yT(PTAP)yf(x)=(Py)^TA(Py)=y^T(P^TAP)y可知，此时得到一个新的二次型g(y)=yTByg(y)=y^TBy，其中B=PTAPB=P^TAP

    二次型进行可逆变换的实质是对其矩阵进行相合变换。

  4. 对于任给的n元二次型f(x)=xTAxf(x)=x^TAx，总有正交变换x=Qyx=Qy，把f(x)f(x)化为标准型g(y)=f(Qy)=λ1y12+λ2y22+⋯+λnyn2g(y)=f(Qy)=\lambda_1y_1^2+\lambda_2y_2^2+\dots+\lambda_ny_n^2，其中λ1,λ1,…,λn\lambda_1,\lambda_1,\dots,\lambda_n是AA的特征值。

惯性定理

  1. 用任何可逆变换x=Pyx=Py将n元二次型f(x)=xTAxf(x)=x^TAx所化为的标准型的正、负平方项的项数都对应相等。
  2. 一个二次型的标准型的正负平方项数分别叫做该二次型的正、负惯性指数。
  3. 用任何相合变换将实对称阵A所化为的对角阵的正、负对角元的个数都对应相等。
  4. 与实对称阵A相合的对角阵的正、负对角元的个数分别叫做A的正、负惯性指数。
  5. 相合的实对称阵A和B具有相同的正、负惯性指数。
  6. 思考题
    1. 若A与B相合，B与C相合，则A与C是否相合？相合。
    2. 两个实对称阵相合的充要条件：正负惯性指数相等。

正定二次型与正定阵

  1. 对于n元二次型f(x)=xTAxf(x)=x^TAx，若对任意的n元非零实向量x，都有f(x)>0f(x)>0，则称f(x)f(x)是正定二次型，并称A为正定阵；若对任意的n元非零实向量x，都有f(x)<0f(x)<0，则称f(x)f(x)是负定二次型，并称A为负定阵。
  2. 若f(x)=xTAxf(x)=x^TAx为n元二次型，则下列命题互为充要条件：
    1. f(x)f(x)为正定二次型，A为正定阵
    2. A的特征值均为正数
    3. A的正惯性指数为n
    4. A相合与单位阵（即存在可逆阵P，使得PAT=EP^AT=E
    5. 存在n阶可逆阵B，使得A=BTBA=B^TB
  3. 若A=(aij)n×nA=(a_{ij})_{n×n}是正定阵，则
    1. A的对角元aii>0(aii=eiTAeiT)a_{ii}>0\enspace(a_{ii}=e_i^TAei^T)
    2. ∣A∣>0|A|>0
  4. A=(aij)n×nA=(a_{ij})_{n×n}的左上角k阶子阵为A的k阶顺序主子阵，记作AkA_k，即Ak=(aij)k×kA_k=(a_{ij})_{k×k}，AkA_k的行列式叫作A的k阶顺序主子式。
  5. 实对称阵A=(aij)n×nA=(a_{ij})_{n×n}为正定阵的充要条件是A的各阶顺序主子式都大于0.

书末结论

  1. 等价变化只保持秩不变；

    相似变换保持行列式、秩、特征值、特征值的符号不变；

    相合变换保持秩、特征值的符号及正定性不变；

    正交相似变换保持行列式、秩、特征值、特征值的符号及正定性都不变。