树状数组的问题模型

朴素的查询区间和+修改操作的时间复杂度为O(1) & O(n)，树状数组将其时间复杂度降低至均为O(logn)。

lowbit函数

顾名思义，lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1，举个例子，x = 6，它的二进制为110，那么lowbit(x)就返回2，因为最后一位1表示2。

两种方法实现：

消除最后一位1，再用原数减去消除最后一位1的数，答案即为lowbit(x)的结果。
用补码来运算。

实现的代码如下：

// 方法1
int lowbit(x) 
{	
    return x - (x & (x - 1));
}
// 方法2
int lowbit(x) 
{	
    return x & -x;
}

树状数组的思想

一些定义：arr是原数组，c是新开的一个数组，这个数组代表后缀和;

二进制的视角：一个数n，假设n = 6，它的二进制为110，我们把它表示成累加的形式110 = 100 + 10，前6(110)项的和可以这样求：

$\sum_{i=1}^6=(arr_1+arr_2+arr_3+arr_4)+(arr_5+arr_6)$

括号中的元素个数，是不是4(100)个加2(10)个，和110 = 100 + 10很像

同时，10就是lowbit(110)的结果，100是lowbit(100)的结果。求和的时候我们总是把 $\sum_{i=1}^n$ 拆分成这样的几段区间和来计算，而如何去确定这些区间的起点和长度呢？就是根据n的二进制来的，二进制怎么拆的，就怎么拆分，而拆分二进制就要用到上面说的lowbit函数了。这里也可以顺理成章得给出c数组的表示了。

例如：

$\sum_{i=1}^6=(arr_1+arr_2+arr_3+arr_4)+(arr_5+arr_6)=(arr_1+arr_2+arr_3+arr_4)+c[6]\\=\sum_{i=1}^4+c[6]=c[6-lowbit(6)]+c[6]$

树状数组的实现

查询

这里说的查询是查询任一区间的和，由于区间和具有可加减性，故转化为求前缀和；

查询前缀和刚刚在树状数组的思想中已经说过了，就是把大区间分成几段长度不等的小区间，然后求和。区间的个数为 $O(logn)$ ，所以查询的时间复杂度为 $O(logn)$

修改

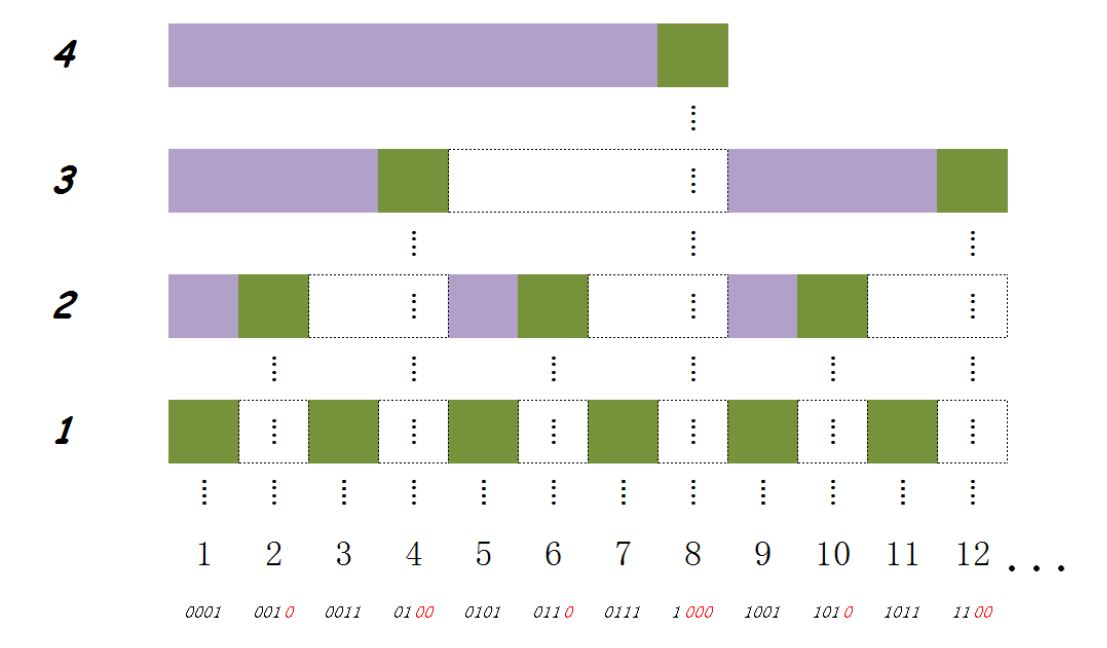
可以得到树状数组的性值：

后缀和的长度是2的幂；
上一层后缀和的长度是下一层后缀和长度的两倍；
一层后缀和只要补上自己后缀和的长度就可以得到上面层的后缀和(图中的虚框框)，注意，是上面的后缀和，而不是上一层的后缀和，这个性质就是更新操作的依据；
最后一位1右边有多少个0(可以用 $log_2(lowbit(x))$ 表示)就表示这一层有多少个直系子层(子层的意思就是这一层的和包含下面某一层的和)。

更新操作：

// 这里的val应该是修改值的变化量
void update(int x, int val, int *c, int n)
{
    for ( ; x <= n; c[x] += val, x += lowbit(x));
}

Leetcode.775 全局倒置与局部倒置

775. 全局倒置与局部倒置 - 力扣（LeetCode）

根据题意，对于每个 $nums[i]$ 而言：

其左边比它大的 $nums[j]$ 的个数，是以 $nums[i]$ 为右端点的“全局倒置”数量，统计所有以 $nums[i]$ 为右端点的“全局倒置”数量即是总的“全局倒置”数量 $a$
同时我们可以将每个 $nums[i]$ 与前一个值进行比较，从而统计总的“局部倒置”数量 $b$ ，其中 ii 的取值范围为 $[1,n−1)$