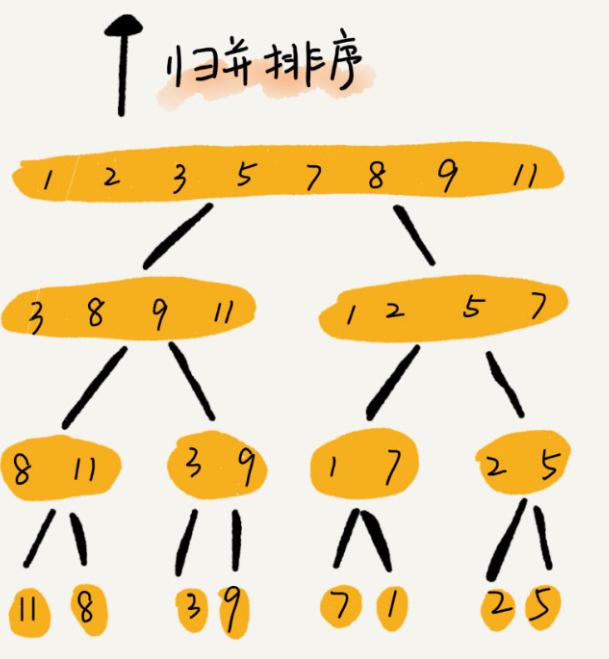
Leetcode 264 丑数

题目描述

给你一个整数 n ，请你找出并返回第 n 个 丑数 。

丑数 就是只包含质因数 2、3 和 5 的正整数。

示例

1
2
3
4
5
6
7
// 输入：n = 10

// 输出：12

// 解释：[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。

// 1 <= n <= 1690

思路

最朴素的思路便是顺序对每个数字进行检测是否为丑数，时间复杂度为O(n2)O(n^2)。

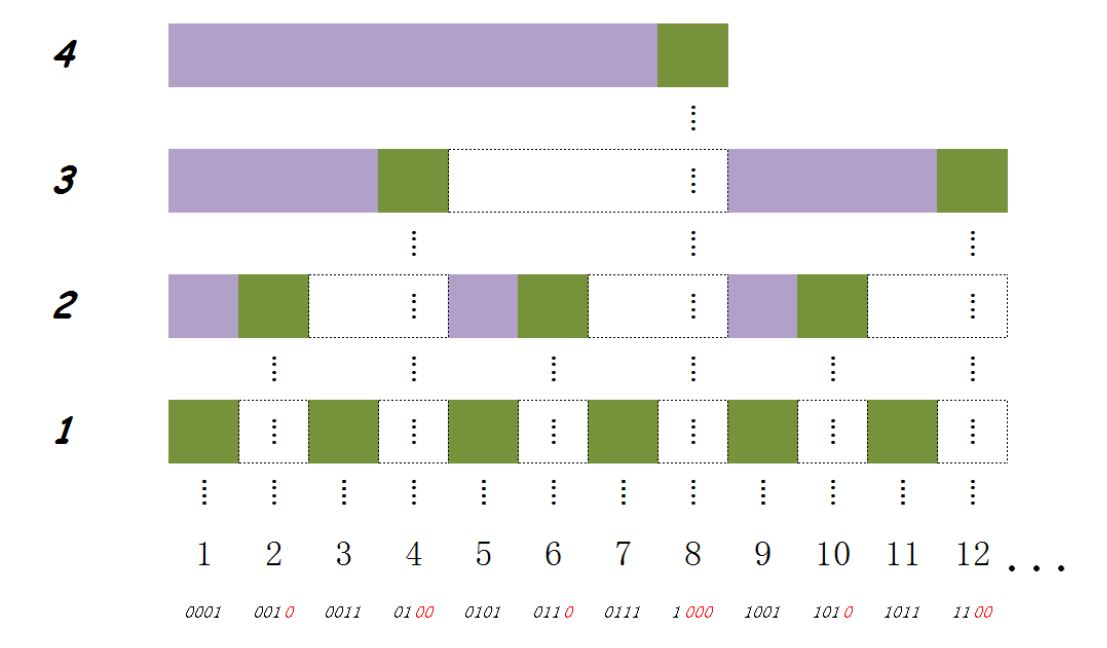
我们可以发现，对于每个丑数xx，2x,3x,5x2x, 3x, 5x均为丑数。

其中，倍数为2的丑数分别为1∗2,2∗2,3∗2,…1*2,2*2,3*2,\dots，即2,4,6,8,…2, 4, 6, 8,\dots，倍数为3的丑数分别为1∗3,2∗3,3∗3,…1*3,2*3,3*3,\dots，即3,6,9,12,…3, 6, 9, 12,\dots，倍数为5的丑数分别为1∗5,2∗5,3∗5,…1*5,2*5,3*5,\dots，即5,10,15,…5,10,15,\dots。

最终的目的便是将这三个数列归并，找到第n个数即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int nthUglyNumber(int n) {
        array<long, 1690> arr;
        arr[0] = 1;
        int p2 = 0, p3 = 0, p5 = 0;
        long now_value = 1;
        for (int i = 1; i < n; i++) {
            now_value = min(arr[p2] * 2, min(arr[p3] * 3, arr[p5] * 5));
            if (arr[p2] * 2 == now_value) p2++;
            if (arr[p3] * 3 == now_value) p3++;
            if (arr[p5] * 5 == now_value) p5++;
            arr[i] = now_value;
        }
        return now_value;
    }
};

Leetcode 373 786 多路归并

这两道题都是多路归并的题，题目特点均为存在两个有序数组，分别从每个数组中取一个元素计算一个值，求出第k大的值与其对应数组中的位置。

解题思路均为采用优先队列，以786为例，问题等价于我们从n−1 个（下标 0 作为分母的话，不存在任何分数）有序序列中找到第 k 小的数值。这 n−1 个序列分别为：

1

起始将第一列入队，然后弹出k次，每次弹出后将同一行的下一个元素入队。时间复杂度为O(nlogn)O(nlogn)(初始插入)+O(klogn)O(klogn)(查找k次)，即max(n,k)∗log(n)max(n, k)*log(n)。

Leetcode 1439 有序矩阵中的第 k 个最小数组和

题目描述

给你一个 m∗nm * n 的矩阵 matmat，以及一个整数 kk ，矩阵中的每一行都以非递减的顺序排列。

你可以从每一行中选出 11 个元素形成一个数组。返回所有可能数组中的第 kk 个 最小数组和。

示例

1
2
3
4
输入：mat = [[1,3,11],[2,4,6]], k = 5
输出：7
解释：从每一行中选出一个元素，前 k 个和最小的数组分别是：
[1,2], [1,4], [3,2], [3,4], [1,6]。其中第 5 个的和是 7 。  
1
2
输入：mat = [[1,3,11],[2,4,6]], k = 9
输出：17
1
2
3
4
输入：mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
输出：9
解释：从每一行中选出一个元素，前 k 个和最小的数组分别是：
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]。其中第 7 个的和是 9 。

数据范围:

  • m==mat.lengthm == mat.length
  • n==mat.length[i]n == mat.length[i]
  • 1<=m,n<=401 <= m, n <= 40
  • 1<=k<=min(200,nm)1 <= k <= min(200, n ^ m)
  • 1<=mat[i][j]<=50001 <= mat[i][j] <= 5000
  • mat[i]mat[i] 是一个非递减数组

思路

同样是多路归并问题，该题进行了多次多路归并，首先将前两行进行归并，得到长度小于等于k的最大和序列，即为前两行相加以后前k大的元素，接着将和序列与下一行继续归并，直到矩阵的最后一行，归并后第k个元素即为所求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Sum {
public:
    int x;
    int y;
    int sum;
    Sum(int ix, int iy, int isum) : x(ix), y(iy), sum(isum) {};
    bool operator<(const Sum& rhs) const{
        return sum > rhs.sum;
    }
};
class Solution {
public:
    vector<int> merge(vector<int> vec1, vector<int> vec2, int k) {
        priority_queue<Sum> q;
        vector<int> ans;
        int l = vec1.size();
        for (int i = 0; i < min(k, l); i++) {
            q.emplace(i, 0, vec1[i] + vec2[0]);
        }
        while (k-- && (!q.empty())) {
            auto t = q.top();
            q.pop();
            ans.push_back(t.sum);
            if (t.y + 1 < vec2.size()) q.push(Sum(t.x, t.y + 1, vec1[t.x] + vec2[t.y + 1]));
        }
        return ans;
    }

    int kthSmallest(vector<vector<int>> &mat, int k) {
        if (mat.size() == 1) return mat[0][k - 1];
        vector<int> prev(mat[0]);
        int now = 1;
        while (now < mat.size()) {
            prev = move(merge(prev, mat[now], k));
            now++;
            // for (int i = 0; i < prev.size(); i++) printf("%d ", prev[i]);
            // printf("\n");
        }
        
        // for (int i = 0; i < v.size(); i++) printf("%d ", v[i]);
        if (prev.size() < k) return prev[prev.size() - 1];
        return prev[k - 1];
    }
};